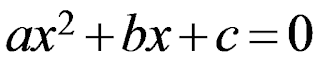Звернення до учнів і батьків.

Доброго дня, шановні учні і батьки!

Звертаюся до вас з проханням швидше виконувати домашні завдання і пересилати їх на електронну адресу dymytrow@ukr.net! Після кожного заняття у блозі є домашня робота. Її потрібно виконувати і пересилати! На розгляд кожного заняття дається 2-3 доби. За цей час можливо встигнути розібрати тему уроку і зробити домашню роботу. До того ж, із-за кількості навчальних предметів, домашнє завдання сконструйовано таким чином, щоб не пере-навантажувати дітей. В результаті, з 20 - 30 учнів класів, працюють, лише, ≈ по 10 учнів. Найбільш активним класом є 6-а, в якому 80% учнів виконують домашні роботи з математики. Активним був і 5-а клас, але, останнім часом, послабив позиції. Найменш активними є 6-б і 8-а класи, в яких працюють лише 40-50% учнів.

Залишається останній місяць навчання, скористуйтеся ним. Підтягніть те, що пропустили. Присилайте роботи, які повинні були прислати. Діти, які не матимуть оцінок по темі, будуть не атестовані. Успіхів!

З повагою, Олександр Володимирович.

8 клас. Геометрія. Контрольна робота.

Перейди за посиланням і виконай тести↓
Многокутники. Площі многокутникув.

6 клас. Паралельні прямі.

Тема. Паралельні прямі.

Мета: ознайомитися з поняттям "Паралельні прямі", навчитися креслити паралельні прямі, ознайомитися з вправами, в яких застосовують паралельні прямі; розвивати логічне мислення, креслярські здібності; виховувати працездатність, любов до математики.

Тип заняття: дистанційне.

Хід заняття.
І. Організаційний етап.
Для  заняття слід підготувати: підручник, зошит, ручку, олівець, лінійку, косинець.

ІІ. Актуалізація опорних знань.
-З чого складається кут?-Що називається прямим кутом?
-Які види кутів ви знаєте?
-Чому дорівнює сума кутів трикутника? Чотирикутника?

ІІІ. Мотивація навчальної діяльності. 
Слово вчителя.
-Доброго дня, діти! Розглянемо тему "Паралельні прямі". Для знайомства з нею вам знадобиться креслярський інструмент: олівець, транспортир, лінійка, косинець. В темі "Паралельні прямі" ви дізнаєтесь, що дві прямі, які не перетинаються, широко використовують у житті як модель конструкторської діяльності людини. 
Малюнки, на яких зображені паралельні прямі, бувають різної складності. Під час заняття ви навчитеся креслити малюнки, які містять паралельні прямі, а також дізнаєтеся про їх застосування у конструкторській діяльності. Успіхів на уроці!

IV. Вивчення нової теми.
За підручником О.С.Істер.
Запиши основні терміни і правила з параграфа 52 в робочий зошит.

V. Розв'язування вправ.

За підручником О.С.Істер.

№1481

На малюнку АBCD - прямокутник. Запиши пари паралельних прямих.

Розв'язання: АВ і CD, АD і ВС.

№1484

Побудуй кут АОВ, градусна міра якого дорівнює 115 градусів. Познач у внутрішній області кута точку D і проведи через цю точку прямі, паралельні променям АО і ВО.

Розв'язання.

VI. Домашнє завдання.

Виконати вправи на сторінці 261 №1479 (письмово), №1483, №1485.

Дякую за увагу! До побачення!

8 клас. Алгебра. Контрольна робота.

Перейди за посиланням↓
Тести. Квадратні рівняння. Теорема Вієта.

5 клас. Середнє арифметичне.

Тема. Середнє арифметичне.

Мета: ознайомитися з поняттям "Середнє арифметичне", навчитися знаходити середнє арифметичне за даними задач; розвивати швидкість і точність у розрахунках; виховувати серйозне ставлення до математики.

Тип заняття: дистанційне.

Хід заняття.
Організаційний етап.
Підготувати до заняття: підручник з математики, зошит, ручку, олівець, лінійку.

Актуалізація опорних знань.
-Як знайти число за даним відсотком? Опишіть письмово.
-Як знайти відсоток за даним числом? Опишіть письмово.

Мотивація навчальної діяльності.
Слово вчителя.
-Доброго дня, діти! Ви ознайомилися з темою "Відсотки" при дистанційних умовах навчання. Вміти розв'язувати задачі на відсотки означає розуміти що є відсотком.
До підсумкової контрольної роботи залишається три тижні. Це час, за який можна тренуватись розв'язувати задачі на відсотки.
Сьогодні ми розглянемо тему, яка називається "Середнє арифметичне". Учні, які знайдуть час плідно попрацювати зараз, зможуть розв'язувати задачі окремого типу на знаходження середнього арифметичного чисел, відсотків, градусів тощо. Успіхів!

Вивчення нового матеріалу.
Число, отримане при діленні суми доданків на кількість доданків, називають середнім арифметичним цих доданків.
Нехай дано три доданки: 13, 46 і 124. Тоді їх сума виглядає так: 13+46+124. Логічно. Сума трьох доданків = 183. І тепер поділимо отриману суму на кількість доданків (три): 183:3=61.
Отримане число 61 є середнім арифметичним трьох доданків 13, 46 і 124!

Розв'язування вправ.
1. Обчисліть середнє арифметичне кутів трикутника.
Розв'язання.
Відомо, що сума кутів трикутника = 180 градусів. Логічно, що в трикутнику кількість кутів дорівнює трьом, отже 180:3=60 градусів. Середнє арифметичне кутів трикутника дорівнює 60 градусам.
2. У Василя виконано 95% домашніх робіт, у Ірини - 90%, у Сашка - 65%, у Марії - 40%. Віталій не зробив жодної домашньої роботи. Знайди середнє арифметичне відсотків виконаних робіт.
Розв'язання.
Сума виконаних домашніх робіт учнями виглядає так: 90%+40%+65%+95%+0% = 290%. Оскільки кількість учнів = 5, то друга дія по знаходженню середнього арифметичного виглядає так: 290%:5=58%. Відповідь: середнє арифметичне виконаних робіт учнями становить 58%.

Домашнє завдання.
Прочитати параграф 44. Виконати вправи на сторінці 256 №1588, №1590. На сторінці 257 №1592; №1599.

Виховна година.

День пам'яті катастрофи на Чорнобильській АЕС.
Статтю узято з: мультимедійна платформа іномовлення України "Укрінформ".

Сьогодні - 34 річниця Чорнобильської катастрофи

26.04.2020 08:06

8 грудня 2016 року Генеральна Асамблея Організації Об'єднаних Націй ухвалила резолюцію,  якою проголосила 26 квітня Міжнародним днем пам'яті про чорнобильську катастрофу.

Як відомо, 26 квітня 1986 року, о 1 год. 23 хв., на четвертому енергоблоці Чорнобильської АЕС стався потужний хімічний вибух, який спричинив руйнування частини реакторного блоку і машинного залу.

Внаслідок вибуху виникла пожежа, яка перекинулася на дах третього енергоблоку. Майже одразу на місце аварії приїхали пожежники. Вогонь гасили до 5 години ранку. Проте, у середині самого четвертого блоку його вдалося ліквідувати лише 10 травня, коли більша частина графіту згоріла.

Після вибуху та пожежі утворилася радіоактивна хмара, яка накрила не лише території сучасної України, Білорусі та Росії, але й території багатьох європейських країн – Швеції, Австрії, Норвегії, Німеччини, Фінляндії, Греції, Румунії, Словенії, Литви, Латвії. За Міжнародною шкалою ядерних подій (INES) цю аварію класифікували за найвищим – сьомим рівнем небезпеки.

Від самого початку Москва та керівництво УРСР приховували факт аварії та наслідки екологічної катастрофи. Першою про підвищення рівня радіації повідомила Швеція. Лише 28 квітня в СРСР з’явилося  перше офіційне повідомлення.

У перші дні після аварії було евакуйоване населення 10-кілометрової зони, надалі зону евакуації розширили до 30 кілометрів. Загалом в Україні радіоактивно забрудненими стали 2293 населених пунктів, у яких на кінець вісімдесятих років минулого сторіччя мешкало понад 2,6 млн осіб. В результаті цієї катастрофи з сільськогосподарського користування було виведено понад 5 млн га земель.

Читайте також: Чорнобиль продовжує про себе нагадувати

Задля запобігання розповсюдженню радіації наприкінці 1986 року зруйнований реактор накрили спеціальним «саркофагом». За оцінками спеціалістів, під ним залишилося близько 95% палива, яке було в реакторі на момент аварії, а також значна кількість радіоактивних речовин, які складаються із залишків зруйнованого реактора. З міркувань безпеки 15 грудня 2000 року роботу Чорнобильської АЕС було припинено. Водночас об’єкт «Укриття», зведений у 1986 році, поступово руйнувався.

Україна звернулася до міжнародної спільноти щодо проведення конкурсу проектів із перетворення об’єкта «Укриття». У 2004 році було проведено тендер на проектування і спорудження нового «саркофагу» -  Нового безпечного конфайнмента. Цей проект повністю профінансовано Європейським банком реконструкції та розвитку: кошти на будівництво, а це близько 1,5 млрд. Євро, надали 40 країн-донорів. Зрештою, 10 серпня 2007 року був підписаний Контракт щодо будівництва НБК, а 29 жовтня 2007 року почалися роботи. До робіт були залучені найкращі українські та зарубіжні фахівці.

29 листопада 2016 року Арку НБК було насунуто на об’єкт «Укриття». Нині Новий безпечний конфайнмент над зруйнованим енергоблоком Чорнобильської АЕС введений в експлуатацію. Надалі будуть роботи з демонтажу нестабільних конструкцій об’єкту «Укриття». За задумом проектувальників, нова споруда зможе вирішити проблему, як мінімум, на сто років, хоча ліквідувати станцію планують у 2065 році.

Чорнобильська трагедія стала символом мужності ліквідаторів, і пам'ятати про їхній подвиг є обов'язком українців.

"26 квітня є Днем пам’яті про найбільшу техногенну катастрофу та вшанування всіх, хто брав участь у ліквідації наслідків аварії на ЧАЕС. Чорнобиль – не лише велика трагедія, а й символ безмежної мужності багатьох тисяч наших земляків", - наголосив голова Державної служби з надзвичайних ситуацій Микола Чечоткін у зверненні з нагоди 34-ї річниці Чорнобильської катастрофи.

Він наголосив, що обов'язок українців пам'ятати про всіх ліквідаторів аварії на Чорнобильській АЕС.

"Ми пам'ятаємо всіх поіменно: і тих хто відійшов у вічність, і тих, з ким маємо честь жити і працювати разом. Низький уклін і довічна шана всім, хто брав участь у подоланні чорнобильського лиха, хто ціною власного життя подарував майбутнє всьому людству", - наголосив Чечоткін і подякував ліквідаторам за їхні мужність, героїзм та самопожертву.

6 клас. Перпендикулярні прямі.

Тема. Перпендикулярні прямі.

Мета: ознайомитися з поняттям "Перпендикулярні прямі", навчитися креслити перпендикулярні прямі, ознайомитися з вправами, в яких застосовують перпендикулярні прямі; розвивати логічне мислення, креслярські здібності; виховувати працездатність, любов до математики.

Тип заняття: дистанційне.

Хід заняття.
І. Організаційний етап.
Для  заняття слід підготувати: підручник, зошит, ручку, олівець, лінійку, косинець.
ІІ. Актуалізація опорних знань.
-Що називається кутом?
-Які види кутів ви знаєте?
-Чому дорівнює сума кутів трикутника? А чотирикутника?
ІІІ. Мотивація навчальної діяльності. 
Слово вчителя.
-Доброго дня, діти! Починаємо розглядати тему "Перпендикулярні прямі". Для знайомства з нею вам знадобиться креслярський інструмент: олівець, транспортир, лінійка, косинець. В темі "Перпендикулярні прямі" ви дізнаєтесь, що дві прямі, які утворюють кут 90 градусів, широко використовують у житті як модель конструкторської діяльності людини. 
Малюнки, на яких зображені перпендикулярні прямі, вчаться креслити усі діти. Коли діти виростають, дехто йдуть вчитися у Вищі навчальні заклади на інженерів- конструкторів, щоб креслити проекти будинків та споруд. На сьогоднішньому уроці ви будете вчитися правильно і чітко креслити перпендикулярні прямі, прямі, що перетинаються під гострими та тупими кутами.
IV. Вивчення нової теми.
За підручником О.С.Істер.

V. Розв'язування вправ.

За підручником О.С.Істер.

№1465.

На малюнку 101 MKPN - прямокутник. Випиши всі пари перпендикулярних прямих.

Розв'язання.

-Перекреслимо малюнок.

Перпендикулярні одна одній прямі: MK i KP; KP i PN; PN i NM; NM i MK.

№1468.

Через точку А, що не належить прямій m, побудуй за допомогою косинця пряму n, перпендикулярну до прямої m.

Розв'язання.

Коси́нець — креслярський інструмент у формі прямокутного трикутника для побудови кутів при виконанні креслеників, схем тощо, або у формі скріплених під прямим кутом брусків для розмічання і контролю кутів у слюсарній справі та деревообробці.

-Робимо креслення за допомогою косинця по умові задачі.

VI. Домашнє завдання.

Виконати вправи на сторінці 258 №1466, №1470.
Дякую за увагу! До побачення!

8 клас. Площа трапеції.

Тема. Площа трапеції.

Мета: сформувати поняття про площу трапеції, навчитися застосовувати формули для знаходження площ трапецій; розвивати практичні здібності, математичну логіку; виховувати любов до геометрії, зацікавленість предметом, цілеспрямованість.

Тип заняття: дистанційне.

Хід заняття.
І. Організаційний етап.
Підготувати підручник, зошит, ручку, олівець, лінійку для заняття геометрією.
ІІ. Актуалізація опорних знань.
-За якою формулою можна знайти кількість діагоналей многокутника?
-За якою формулою можна знайти суму кутів многокутника?
-Запишіть формули радіусів описаного навколо чотирикутника і вписаного в чотирикутник кіл.
ІІІ. Мотивація навчальної діяльності. 
Слово вчителя.
-Шановні восьмикласники! На жаль, вас мотивувати навчатися стає все складніше і складніше. Багато хто з вас знає, що буде здавати наступного року ДПА, а через три роки - ЗНО.  Із-за цього, любі діти, мотивувати не потрібно. Батьки вам допоможуть у подальшому житті: одних влаштують вчитися у вищих навчальних закладах, інших - у технікуми, академії, ліцеї. Комусь з вас, можливо,доведеться вийти заміж або одразу влаштуватися на роботу, не отримуючи спеціальної освіти тощо. У будь-якому випадку, в майбутньому вам потрібно зробити крок у життя! Найбільша ваша допомога - це ваші знання. Чим більше ви знаєте, тим більше вмієте, а чим більше вмієте - тим більше користі від вас.
Сподіваюся, що ця промова надихне вас, шановні учні, і ви розглядатимете дистанційне навчання не через призму рожевих окулярів, а як люди, які починають самостійно нести відповідальність за свої знання, вчинки і оцінки.
IV. Вивчення нового матеріалу.
За підручником О.С. Істер.
-Прочитайте параграф 26. Запишіть у свій зошит теорему про площу трапеції та її наслідокки. Випишіть формули для знаходження площі трапеції. Вивчіть теорему і формули.

-Також можна обчислювати площі трапецій, знаючи і застосовуючи інші формули. Якщо вам цікаво знати які, пишіть у коментарях до даного заняття. А поки розглянемо більш стандартну формулу для знаходження площі трапеції на практиці.

V. Розв'язування вправ.
За підручником О.С. Істер.
№ 967.
Менша основа рівнобічної трапеції = 10 од. Точка перетину діагоналей віддалена від основ на 2 од і 3 од. Знайдіть площу трапеції.
Розв'язання:
-Накреслимо рівнобічну трапецію та перетин діагоналей в ній.

-Дано рівнобічну трапецію АВСD. АС і ВD - діагоналі трапеції. Точка О - перетин діагоналей. Прямі ЕО і FО - відстань від точки перетину діагоналей до основ трапеції. ВС = 10. ЕО = 2. FО= 3. ЕО+FО=Н трапеції. Тобто, висота трапеції дорівнює 2+3.

Подивіться на два прямокутних трикутника ОЕС і ОFD. Вони подібні за ознакою подібності трикутників, де кут при вершині FОD є рівним куту при вершині ЕОС. Завдяки знанням з пройденої теми про подібність трикутників складаємо пропорцію сторін трикутників: СЕ:DF=ЕО:FO.  5:Х=2:3.  2Х=15.  Х=7,5.

В параграфі 26 ви ознайомилися з теоремою про площу трапеції і вже знаєте, що площа трапеції дорівнює добутку середньої лінії трапеції на висоту. 

Середня лінія трапеції - це сума основ поділена на два. L=ВС+АD/2 = 10+15/2 = 25/2 = 12,5 од.

Площа - це добуток середньої лінії трапеції на висоту. S=H×L = 5×12,5 = 62,5 од.

VII. Домашнє завдання.

Відповісти на запитання цього заняття. Виконати вправи на сторінці 180 №966, №968.

Дякую за увагу!

5 клас. Тест. Відсотки.

Перейди за посиланням↓

Тест. Відсотки.

6 клас. Контрольна робота з теми "Рівняння".

Контрольна робота з теми "Рівняння".

1. Розв'яжи рівняння.

2. За умовою задачі склади рівняння і розв'яжи його.
У родині шість осіб. Батько старше матері на 4 роки, так само, на 4 роки, старший син старше середнього. Старший син вдвічі молодше матері, а середній - втричі старше доньки. А донька вдвічі молодша від молодшого сина. По скільки років кожному з членів родини, якщо в сумі усім шістьом 192 роки?

Шановні учні! Надсилайте свої роботи на електрону скриньку dymytrow@ukr.net.

8 клас. Розв'язування квадратних рівнянь.

Тема. Розв'язування квадратних рівнянь.

Мета: розглянути вправи із застосуванням квадратних рівнянь, навчитися розв'язувати вправи; розвивати математичну компетентність; виховувати прагнення розв'язати найскладнішу вправу.

Тип заняття: дистанційне.

Хід заняття.
Слово вчителя.
-Доброго дня, учні і учениці. Пропоную розглянути дистанційне заняття розв'язування вправ. Вчитель розв'язує вправу і дає наступну вправу, подібну розв'язаній, для розв'язання учням.

Розв'яжи квадратне рівняння.
За підручником О.С. Істер.
№880. Задача. До Різдва всі члени родини Петренків підготували одне одному подарунки та поклали їх під ялинку. Скільки осіб у родині Петренків, якщо під ялинкою виявилося 20 подарунків?
-В умові задачі пропонується застосувати квадратне рівняння, як математичну модель текстової задачі, та розв'язати рівняння, тим самим розв'язавши задачу.
Спочатку потрібно задати невідому змінну. Позначимо усіх членів родини літерою "х". Коли кожен член родини підготував кожному по подарунку, то подарунків від одного члена родини стало "х-1", тому що собі подарунок ніхто із членів родини дарувати не буде. Отже, ми можемо тепер скласти рівняння, помноживши усіх членів родини на кількість виготовлених подарунків кожним членом родини, та розв'язати його.

Відповідь: у родині 5 осіб.
-Тепер, восьмикласники, настала ваша черга розв'язувати квадратне рівняння!
Розв'яжи квадратне рівняння:
х(х + 10) = 24.

5 клас. Розв'язування задач на відсотки.

Тема. Знаходження числа за його відсотком.

Мета: розглянути задачі із застосуванням відсотків, навчитися розв'язувати задачі; розвивати математичну компетентність; виховувати прагнення розв'язати найскладнішу задачу.

Тип заняття: дистанційне.

Хід заняття.
Слово вчителя.
-Доброго дня, учні і учениці. Пропоную розглянути дистанційне заняття розв'язування задач. Вчитель розв'язує задачу і дає наступну задачу, подібну розв'язаній, для розв'язування учням.

Розв'яжи задачу.
За підручником О.С. Істер.
№1567.
Витративши 35% бензину, що був у баку, шофер побачив що в ньому залишилося 36,4 л бензину. Скільки літрів бензину було у баку спочатку? Скільки літрів витратив шофер?
-Діти, вам відомо, що будь-яка множина складається зі ста відсотків. Множина літрів бензину у баку також. Якщо ми віднімемо від усієї множини літрів бензину у баку 35%, витрачених шофером, то отримаємо першу дію розв'язання задачі:
1)100%-35%=65%.
-Відомо, що у шофера залишилося 36,4 літрів бензину, що у відсотках дорівнює якому числу, як ви думаєте? 36,4 л = 65% бензину у баку. Переведемо 65% у десятковий дріб: 65%=0,65. Поділимо кількість залишених літрів бензину на переведений десятковий дріб:
2)

-Ви бачите, які операції я зробив у другій дії розв'язання задачі? Спочатку перевів десяткові дроби у звичайні, потім перевів мішане число у неправильний дріб, а другий звичайний дріб скоротив на 5. Далі, щоб поділити два звичайних дроби, необхідно їх помножити, перевернув чисельник на знаменник у другому звичайному дробі. Потім дроби скорочуються і отриманий результат є відповіддю!

3) 56-36,4=19,6

Відповідь: бак розраховано на 56 літрів бензину; шофер витратив 19,6 літрів бензину.

-Учні, задачу, записану нижче, розв'яжіть самостійно!

Під час сушіння, яблука втрачають 82% своєї маси. Скільки треба взяти свіжих яблук, щоб отримати 261 кг сушених?

6 клас. Розв'язування рівнянь.

Тема. Розв'язування рівнянь.

Мета: розглянути рівняння із застосуванням розподільної властивості множення, навчитися розв'язувати рівняння; розвивати математичну компетентність; виховувати прагнення розв'язати найскладніше рівняння.

Тип заняття: дистанційне.

Хід заняття.
Слово вчителя.
-Доброго дня, учні і учениці. Пропоную розглянути дистанційне заняття розв'язування рівнянь. Вчитель розв'язує рівняння і дає наступне рівняння, подібне розв'язаному, для розв'язання учням.
Розв'яжи рівняння:

-Якщо коефіцієнти а=0 і b=0, то рівняння має безліч розв'язків.
Відповідь: безліч розв'язків.
-Переходимо до наступного рівняння:

-Якщо коефіцієнти а=0 і b≠0, то рівняння розв'язків не має.
Шановні діти, а рівняння, яке записано нижче, розв'яжіть самостійно!

8 клас. Площа трикутника.

Тема. Площа трикутника.

Мета: сформувати поняття про площу трикутника, навчитися застосовувати формули для знаходження площ трикутників; розвивати практичні здібності, математичну логіку; виховувати любов до геометрії, зацікавленість предметом, цілеспрямованість.

Тип заняття: дистанційне.

Хід заняття.
І. Організаційний етап.
Підготувати підручник, зошит, ручку, олівець, лінійку для заняття геометрією.
ІІ. Актуалізація опорних знань.
-За якою формулою можна знайти кількість діагоналей многокутника?
-За якою формулою можна знайти суму кутів многокутника?
-Запишіть формули радіусів описаного навколо трикутника і вписаного в трикутник кіл.
ІІІ. Мотивація навчальної діяльності. 
Слово вчителя.
-Шановні восьмикласники! На жаль, вас мотивувати навчатися стає все складніше і складніше. Багато хто з вас знає, що буде здавати наступного року ДПА, а через три роки - ЗНО.  Із-за цього, любі діти, мотивувати не потрібно. Батьки вам допоможуть у подальшому житті: одних влаштують вчитися у вищих навчальних закладах, інших - у технікуми, академії, ліцеї. Комусь з вас, можливо, доведеться вийти заміж або одразу влаштуватися на роботу, не отримуючи спеціальної освіти тощо. У будь-якому випадку, в майбутньому вам потрібно зробити крок у життя. Найбільша ваша допомога наразі - це ваші знання. Чим більше ви знаєте, тим більше вмієте, а чим більше вмієте - тим більше користі від вас.
Сподіваюся, що ця промова надихне вас, шановні учні, і ви розглядатимете дистанційне навчання не через призму рожевих окулярів, а як люди, які починають самостійно нести відповідальність за свої знання. вчинки і оцінки. Вперед вивчати нову тему!
IV. Вивчення нового матеріалу.
За підручником О.С. Істер.
-Прочитайте параграф 25. Запишіть у свій зошит теорему про площу трикутника та її наслідки. Випишіть формули для знаходження площ трикутників. Вивчіть теорему і формули.

V. Розв'язування вправ.
За підручником О.С. Істер.
№935.
Відрізки АВ і СD перетинаються в точці О, яка є серединою відрізка АВ. Знайдіть відношення площ трикутників АОС і ВОD, якщо СО = 3 см, DО = 6 см.
- Діти, побудуємо малюнок за даною умовою задачі.

-Хоча задача у підручнику котується високим рівнем, уважно прочитавши параграф 25, з її розв'язанням труднощів не виникне. Для цього нам потрібно було зробити правильний малюнок і згадати наслідки з теореми про площу трикутника. Малюнок накреслили, тепер щодо наслідків! В одному з них сказано, цитую: "Якщо сторона одного трикутника дорівнює стороні другого, то площі таких трикутників відносяться як їх висоти, проведені до цих сторін". У нас є відрізок АВ, який поділено навпіл точкою О. Це дає змогу зрозуміти, що сторони АО і ОВ, двох різних трикутників АОС і ВОD, рівні. Висоти, проведені до сторін АО і ОВ дорівнюють 3 см і 6 см відповідно. Отже, площі трикутників АОС і ВОD відносяться як їх висоти СО і DО відповідно. Відповідь: площі трикутників АОС і ВОD відносяться як 3:6 або, скоротивши числа на три, 1:2.

VІ. Домашнє завдання.

За підручником О.С. Істер.

Вивчити теорему про площу трикутника та її наслідки. Вивчити формули площ трикутників. Застосувати формули у вправах на сторінці 175, а саме у №918; 923.

Дякую за увагу! Бережіть себе. До побачення!

5 клас. Знаходження числа за його відсотком.

Тема. Знаходження числа за його відсотком.

Мета: повторити поняття "відсотки"; продовжити формувати уявлення про застосування відсотків у повсякденному житті; навчитися знаходити число за його відсотком; розвивати логічне мислення, послідовність дій; виховувати зацікавленість до математики, старанність при виконанні вправ, точність у розрахунках.

Тип заняття: дистанційне.

Хід заняття.
Організаційний етап.
Підготувати підручник, зошит, ручку, олівець.

Актуалізація опорних знань.

Дайте письмові відповіді на запитання:
-Як перетворити звичайний дріб у відсотки?
-Який алгоритм дій потрібно застосувати, щоб знайти відсоток за його числом?
-Знайди 6%, якщо 40% - це число 200.

Мотивація навчальної діяльності.
-Доброго дня, п'ятикласники та п'ятикласниці! Сподіваюся вам вдається розв'язувати вправи, в яких потрібно знаходити відсоток від заданого числа. Сьогодні потрібно навчитися знаходити число за його відсотком! Маючи компетентність знаходити число за його відсотком ви зможете розв'язувати різні за складністю задачі згідно сьогоднішньої теми! Задачі з застосуванням відсотків широко застосовуються у різних сферах людської діяльності.  Тому, шановні учні і учениці, серйозно поставтеся до засвоєння матеріалу, адже після його опрацювання ви отримаєте оцінки, які покажуть ваші дистанційні старання. Будьте уважні! Приємного заняття!

Засвоєння нового матеріалу.
За підручником О.С. Істер

Розв'язування вправ.

Виконай письмово вправи.

За підручником О.С. Істер

1) Знайдіть число, якщо 12,5% його дорівнює 7,5.

Розв'язання.

Виразимо відсоток у вигляді десяткового дробу: 12,5%=0,125. Тепер число 7,5 поділимо на 0,125. 

Спочатку переводимо число 0,125 в звичайний дріб. При діленні числа 7,5 на звичайний дріб, звичайний дріб перевертається, а знак ділення змінюється на знак множення. Отримаємо відповідь - число 60. Таким чином можна знайти число за його відсотком.

2) Супермаркет протягом трьох днів продавав завезені огірки. Першого дня продали 35% усіх огірків, другого - 38%, а третього - решту 151,2 кг. Скільки кілограмів огірків було завезено до супермаркету?

Розв'язання.

-Обчислимо, скільки відсотків має кількість проданих огірків третього дня. Віднімемо від 100% кількість проданих огірків першого і другого днів: 100%-35%-38%=

=27%.

Отже, 151,2 кг огірків складає 27%.

Виразимо 27% через десятковий дріб: 27%=

=0,27.

Поділимо 151,2 на 0,27.

-Переносимо в обох десяткових дробах кому вправо на стільки цифр, скільки потрібно щоб дільник перетворився на натуральне число.

Записуємо два натуральних числа у вигляді неправильного звичайного дробу.

Починаємо скорочувати звичайний дріб на натуральне число 3 (і чисельник, і знаменник, скорочуються).

В результаті отримуємо число 560, яке характеризує кількість кілограмів огірків, завезених до супермаркету.

Домашнє завдання.

За підручником О.С. Істер

Опрацювати параграф 43. Повторити параграф 42.

Виконати вправи: №1538; №1550; №1559.

Дякую за увагу! Бережіть себе! До побачення!

6 клас. Розв'язування рівнянь за допомогою задач.

Тема. Розв'язування рівнянь за допомогою задач.

Мета: навчитися розв'язувати задачі способом розв'язування рівнянь; розвивати критичне мислення; виховувати зацікавленість.

Тип заняття: дистанційне.

Хід заняття.
Організаційний етап.
Підготувати підручник, зошит, ручку, олівець.
Актуалізація опорних знань.
-Які види рівнянь ви знаєте? Чим вони відрізняються?
-Зробіть перелік назв множин чисел.
Мотивація навчальної діяльності.
Слово вчителя.
-Доброго дня, школярики! Вам відомо, що деякі задачі розв'язуються за допомогою фігур, таких як трикутник, прямокутник, коло, квадрат. В задачах про фігури потрібно знаходити довжини сторін, периметри, площі. Величини знаходять за допомогою сталих формул. Ці формули застосовуються і в змістах розв'язку текстових задач, де потрібно розв'язати рівняння, щоб отримати величину.
Є задачі, в умовах яких йде мова про: подолання відстані, виконану роботу, витрачені гроші тощо. Переліковані величини також мають формули, які потрібно застосовувати у розв'язках рівнянь.
Ми навчимося будувати рівняння за умовою задачі. А потім розв'яжемо його. Вперед!
Вивчення нового матеріалу.
За підручником О.С.Істер

Розв'язування задач.

За підручником О.С.Істер

1) У першому вагоні в 1,5 раза більше вугілля, ніж у другому. Якщо з першого вагона взяти 2,9 тони, а в другий додати 7,1 тони, то вугілля у вагонах стане порівну. Скільки тонн вугілля в кожному вагоні?

Розв'язання.

-Дамо двом вагонам такі буквені вирази, що відповідатимуть кількості тонн вугілля в умові задачі: 3х і 2х (одна кількість в 1,5 раза більша за другу). Тепер складемо рівняння так, щоб кількість вугілля одного вагона була у лівій частині рівняння, а кількість вугілля другого - у правій: 3х = 2х. Зробимо тепер так, щоб вони насправді дорівнювали одна одній: 3х - 2,9 = 2х + 7,1. Розв'язавши це рівняння ми отримаємо число 10, яке є коренем рівняння.

2) У двох маршрутних таксі їхала однакова кількість пасажирів. Після того як з першого таксі вийшло 4 пасажири, а з другого - 12, пасажирів у першому залишилося удвічі більше, ніж у другому. Скільки пасажирів було у кожному таксі спочатку?

Розв'язання.

-Нехай кількість пасажирів в двох таксі дорівнювала одна одній, тоді запишемо це так: а=а.

На зупинці пасажири вийшли з обох таксі: а-4=а-12. Але в першому залишилось удвічі більше пасажирів, тому до множимо правий вираз на 2: а-4 = (а-12)2.  Тоді а = 20.

Шановні учні, дуже сподіваюсь, що вам ця інформація принесла користь і ви зможете самостійно скласти рівняння за умовою задачі і розв'язати його.

Домашнє завдання.

Виконати вправи: сторінка 244 №1369; 1371, сторінка 246 №1387; 1388.

До нових зустрічей!

8 клас. Квадратне рівняння як математична модель текстових і прикладних задач.

Тема. Квадратне рівняння як математична модель текстових і прикладних задач.

Мета: розглянути задачі, які розв'язуються за допомогою квадратних рівнянь, формувати навички інтерплетаціїї умови задачі в її розв'язок, вчитися розв'язувати рівняння; розвивати конструкторські здібності, логічне мислення, математичний погляд на побудову моделі; виховувати відповідальність і прагнення до точного результату.

Тип заняття: дистанційне.

Хід заняття.
І. Організаційний етап заняття.
Підготувати підручник, зошит, ручку. Записати "класна робота у зошиті". Відповісти на запитання актуалізації опорних знань.
ІІ. Актуалізація опорних знань.
-Чим теорема Вієта є корисною у нашому житті?
-Які формули запровадив у своїй теоремі Франсуа Вієт?
-Чому дорівнює сума і добуток коренів не зведеного квадратного рівняння?
ІІІ. Мотивація навчальної діяльності.
Слово вчителя.
-Доброго дня! На попередніх уроках ми розглядали квадратні рівняння виду

 та умови, при яких такі квадратні рівняння можна розв'язувати. Ми вивчили декілька важливих формул для розв'язування квадратних рівнянь та навчилися їх застосовувати.
На сьогоднішньому занятті нам потрібно зробити ще один крок до опанування теми "Квадратні рівняння", а саме: навчитися самостійно складати квадратні рівняння, читаючи умови текстових і прикладних задач! Для досягнення цієї мети нам потрібно прочитати параграф 23 у навчальному посібнику "Алгебра" та самостійно виконати декілька вправ.
IV. Вивчення нового матеріалу.
За підручником О.С.Істера

V. Розв'язування вправ.

1) Добуток двох послідовних натуральних чисел на 181 більший за їх суму. Знайдіть ці числа.

Розв'язання.

-Вам всім відомо, що називається добутком та сумою двох чисел. В умові цієї задачі числа не відомі, але відомо, що ці числа - послідовні. Якщо ми позначимо одне невідоме число літерою "х", то друге число, як послідовне, потрібно позначити виразом "х+1". Тепер складемо квадратне рівняння за умовою задачі, застосовуючи буквені вирази.

Розглянемо число "14" та послідовне число "14+1". Їх добуток 14⋅15=210. Сума послідовних чисел 14+15=29. Добуток більший за суму на 210-29=181. Рівняння побудовано правильно. Відповідь "14".

2) Площа прямокутного листа фанери дорівнює 300 (кв.од.). Його розрізали на дві частини, одна з яких - квадрат, а друга - прямокутник. Знайдіть сторону квадрата, якщо сторона одержаного прямокутника, що не є стороною квадрата, дорівнює 5 (од.).

Розв'язання.

Накреслимо, спочатку, прямокутник та поділимо його так, як запропоновано в умові задачі.

Якщо зробити правильну математичну модель, то скласти рівняння за нею не так уж і складно!

Повністю сторона прямокутника дорівнюватиме "5+х". Тоді S = x⋅(5+x). Відомо, що S = 300. Отже, 

Число "15" задовольняє рівняння, бо 15⋅20=300.

VI. Домашнє завдання.
Дати відповіді на запитання в розділі ІІ."Актуалізація опорних знань". Виконати вправи за підручником: сторінка 194, №875; 876.
До побачення!

5 клас. Задача - гра "100%".

Тема. Відсотки.

Мета: закріпити у своїх знаннях поняття про "відсотки", продовжити формувати уявлення про застосування відсотків у повсякденному житті, навчитися застосувати відсотки у власних прикладах та при розв'язуванні вправ; розвивати арифметичні здібності, між предметні зв'язки, грамотне читання математичних прикладів; виховувати спрямованість до точності у розрахунках.

Тип заняття: дистанційне.

Задача - гра. Перейди за посиланням↓

Задача - гра "100%"

8 клас. Площа паралелограма. 2.

Тема. Площа паралелограма.

Мета: навчитися креслити паралелограм та розв'язувати його за формулами, обчислюючи числові значення величин; розвивати математичне мислення, уяву; виховувати любов до предмету, охайність.

Тип заняття: дистанційне.

Задача. Перейди за посиланням↓
Площа паралелограма.2.

6 клас. Рівняння. Урок 2.

Тема. Рівняння.

Мета: поглибити знання з застосування властивостей при розв'язуванні рівнянь, навчитися компонувати математичні зв'язки та розв'язувати рівняння; розвивати в собі усвідомлення математичної сталості; виховувати снагу до розв'язування рівнянь.

Тип заняття: дистанційне.

Ключові поняття.
Подібні доданки - це такі, як -9е і 5е;  або  3д і -д  або  -2у і -0,71у.
Зведення подібних доданків - це виконання арифметичних дій між коефіцієнтами з буквеними виразами. У поєднанні коефіцієнт та буквений вираз називаються одночленом. Арифметичні дії між одночленами утворюють створення многочленів. Така термінологія починає застосовуватись після вивчення розподільної властивості множення.
Розподільна властивість множення - це знаходження спільного множника у вигляді коефіцієнта або буквеного виразу або поєднання їх та винесення його за дужки, в яких залишається арифметична дія двох чи більше доданків.

Перейди за посиланням↓
Рівняння.2.

Опитування для батьків.

https://docs.google.com/forms/d/e/1FAIpQLSdYg1xf7N7lUVagouEJbWABWfy-4jaBOlD86yFGb7VfOpH1Tg/viewform

8 клас. Площа паралелограма.

Тема. Площа паралелограма.
Мета: ознайомитися з площею геометричної фігури "паралелограм", вміти створювати математичне уявлення про застосування паралелограмів, навчитися вимірювати площу паралелограмів; розвивати креслярські здібності, витримку до креслення об'єкту; виховувати відповідальність за навчання.
Тип заняття: дистанційне.
Хід заняття.
І. Організаційна частина.
Підготувати: зошит, олівець, лінійку, транспортир, гуму.
ІІ. Актуалізація опорних знань.
*Для чого потрібні знання з математики?
*Що таке площа?
*Чому дорівнює сума кутів ен-кутника?
ІІІ. Мотивація навчальної діяльності.
-Шановні учениці і учні, добридень!!! Мотивація буде складатися з наступного перебігу подій: до кінця карантину розглянемо чотири важливі заняття; на кожному занятті ви зможете заробити максимум три бали: за відповіді на питання у розділі уроку "ІІ. Актуалізація опорних знань." - 1,5 бала (0,5 за кожне питання); за теоретичну відповідь по заняттю - 0,5 бала; за домашню роботу - один бал. Усі свої роботи ви повинні залишати у коментарях до відповідного заняття. Будь-ласка, дотримуйтесь правил і виконуйте завдання, працюючи над отриманням балів. Успіхів всім вам, шановні.
IV. Вивчення нового матеріалу.
Площу паралелограма можна обчислити за формулою:

Тепер заходимо в програму Paint і креслимо паралелограм.

V. Теоретичне завдання.

Згадай ознаки і властивості паралелограма.

VI. Практичне завдання.

Накресли в зошиті паралелограм за розмірами і умовою, як зображено на фотографії, застосовуючи креслярські інструменти. Перепиши розв'язання задачі по вимірюванню площі паралелограма через застосування іншої формули площі. Вивчи формулу, яка на фотографії.

VII. Домашнє завдання.

Знайти площу трикутника АDF. 

8 клас. Теорема Вієта.

Тема. Теорема Вієта.

Мета: ознайомитися з властивістю зведених квадратних рівнянь, яка отримала назву "теорема Вієта"; навчитися формулювати властивість зведених квадратних рівнянь самостійно; у повному обсязі усвідомлювати важливість застосування теореми Вієта; вміти знаходити корені зведених квадратних рівнянь користуючись теоремою Вієта; розвивати логічне мислення, математичний світогляд, прагнення до точного результату; виховувати повагу до навчання, цілеспрямованість.

Тип заняття: дистанційне.

Хід заняття.
Про Франсуа Вієта. 
За матеріалом, узятим з Вікіпедія.
Франсуа Вієт - французький математик, що запровадив сучасну систему нотації в алгебрі. Народився 1540 року на півдні Франції у невеликому містечку Фонтене-ле-Конт провінції Пуату. Головною пристрастю Вієта була математика. Він глибоко вивчив твори класиків: Архімеда й Діофанта; найближчих попередників Кардано, Бомпеллі, Стевіна та інших. Майже всі дії й знаки записувалися словами, не було навіть натяку на ті зручні, майже автоматичні правила, якими ми зараз користуємось. Не можна було записувати, і, отже, вивчати в загальному вигляді алгебраїчні рівняння або якісь алгебраїчні вирази. Кожен вид рівняння з числовими коефіцієнтами розв'язувався за особливим правилом. Так, у Кардано розглядалося 66 видів алгебраїчних рівнянь. Тому необхідно було довести, що існують такі загальні дії над усіма числами, які від самих чисел не залежать. Вієт та його послідовники встановили, що не має значення, чи буде розглянуте число кількістю предметів або довжиною відрізка. Головне, що над цими числами можна виконувати алгебраїчні дії й у результаті знову отримати такі ж числа. Отже, їх можна позначати якимись абстрактними знаками. Вієт це й зробив. Він не лише запровадив символьне обчислення, але й зробив принципово нове відкриття, поставивши перед собою мету вивчати не лише числа, а й дії над ними. Щоправда, у самого Вієта алгебраїчні символи були ще мало схожі на наші. Зі знаків дій він використовував «+» і «-», знак радикалу й горизонтальну риску для ділення. Добуток позначав словом «in». Вієт першим став застосовувати дужки, які в нього мали вигляд риски над многочленом. Але багато знаків, які були введені до нього, він не використовував (квадрат, куб тощо), а позначав словами або першими літерами слів. Основу свого підходу Вієт називав видовою логістикою. Наслідуючи приклад античних учених, він чітко розмежував числа, величини та відношення, зібравши їх у деяку систему «видів». До цієї системи входили, наприклад, змінні, їх корені, квадрати, куби і т. д. Для цих видів Вієт дав особливу символіку, позначивши їх маленькими літерами латинської абетки. Для невідомих величин застосовувалися голосні літери, для змінних — приголосні. Вієт довів, що, оперуючи з символами, можна отримати результат, який буде придатним до будь-яких величин, тобто, можна розв'язати задачу в загальному вигляді. Це поклало початок докорінним змінам у розвитку алгебри: стало можливим символьне обчислення. Не випадково, що за це Вієта називають «батьком» алгебри, основоположником літерної символіки.

Про теорему Вієта.

Особливо пишався Вієт відомою теоремою про залежність між коренями квадратного рівняння та його коефіцієнтами, яку він отримав самостійно, хоча, як нині відомо, залежність між коефіцієнтами й коренями рівняння (навіть загальнішого вигляду, ніж квадратне) була відома ще Кардано, а в такому вигляді, як ми застосовуємо її для квадратного рівняння, — давнім вавилонянинам. Теорему було оприлюднено 1591 року. Її названо ім'ям Вієта, а сам автор формулював її так: «Якщо B+D, помножене на А, мінус А в квадраті дорівнює BD, то А дорівнює В і дорівнює D». Теорема Вієта стала зараз одним з найвідоміших тверджень шкільної алгебри. Теорема Вієта варта уваги тим, що її можна узагальнити для многочленів будь-якого степеня.

Помер Франсуа Вієт 14 лютого 1603 року.

Актуалізація опорних знань.

1) Які рівняння називаються зведеними?

2) Що називається коефіцієнтами квадратного рівняння?

3) Наведіть приклад неповного квадратного рівняння.

4) Що називається дискримінантом?

5) Які формули потрібно знати, щоб знайти корені квадратних рівнянь?

Шановні восьмикласники! На питання відповідати потрібно обов'язково! Свої відповіді залишайте у коментарях до даного заняття та заробляйте бали за дистанційну роботу.

Вивчення нового матеріалу.

За підручником О.С. Істера алгебра, 8 клас.

Застосування теореми Вієта під час розв'язування вправ.

Домашнє завдання.

За теоремою Вієта знайдіть корені рівнянь:

*Виконану домашню роботу прикріплюй у коментарях до даного уроку.