Тема. Задання функції.
Доброго дня! На попередньому уроці ми дізналися, що функції можна задавати формулами, наприклад
Дивлячись на формули мимовільно виникає питання: "Як задати функцію формулою?". Уявімо, що тіло рухається у деякому напрямку. Нехай швидкість руху дорівнює один метр за одну секунду. Тоді ми можемо задати функцію за формулою y = x. Чому? З попереднього заняття ми знаємо, що x - це аргумент, тобто незалежна змінна, а y - функція, залежна змінна. Функція (y) змінюється, коли змінюється аргумент. Якщо час іде і пройшло, наприклад, 10 секунд, то тіло відповідно подолає 10 метрів. Якщо пройде дві хвилини, то тіло, стало рухаючись, подолає 120 метрів. Тому формула y = x підходить для задання такої функції, де кількість пройдених секунд дорівнює кількості пройдених метрів.Давайте розглянемо випадок, якщо тіло рухатиметься швидше! Наприклад, 5 метрів за секунду! Тоді задати функцію ми можемо за такою формулою y = kx. Чому? Якщо аргумент показує час, а функція - шлях, який долає тіло за деякий час, то літера "k" показує коефіцієнт. В нашій умові коефіцієнт дорівнює числу 5 (5 метрів за секунду). Тому, якщо тіло перебуває у русі 10 секунд, то подоланий ним шлях дорівнюватиме 5۰10 (метрів). Тоді, наприклад, через сто секунд тіло подолає 500 метрів. Вам зрозуміле таке формулювання??
Працюємо з підручником.
№792.
У першому завданні номера 792 ми підставляємо у формулу запропоновані умовою значення аргумента та знаходимо відповідно єдині значення функції.У другому завданні ми підставляємо у формулу запропоновані умовою значення функції та, виконуючи арифметичні дії, знаходимо відповідні значення аргументів.
№800.
Уважно прочитаємо умову завдання та задамо формулами функції!
1) у = х - 3;
2) у = 2х +5.
В цьому завданні потрібно звертати увагу на слова "в скільки разів більше або менше", "на скільки разів більше або менше", "подвоєні", "потроєні" і т.д. і т.п..
Домашнє завдання.
Прочитати параграф №20; №21.
Відповісти на запитання (письмово):
Що називається залежною змінною? Що називається незалежною змінною? Наведіть приклад та задайте формулою функцію. Що таке область визначення функції? Що таке область значень функції? Яким чином функцію можна позначити інакше?
Виконати №794; №796; №799.
Дякую за увагу! До побачення!

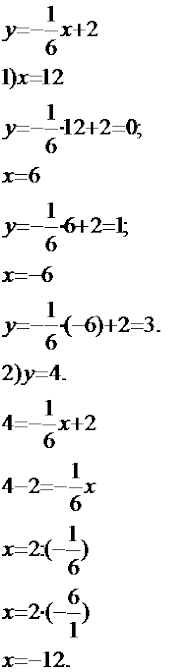
Немає коментарів:
Дописати коментар